What is Eigenvectors & Eigenvalues?

Eigenvectors and Eigenvalues:

we have :

Now, let's say we apply linear transformation:

It moves the original vector i^ to the coordinates [3, 0] & j^ to [1, 3]

so it's represented with a matrix whose columns are

| 3 1 |

|0 2 |

let's focus on what it does to one particular vector and think about the span of that vector, the line passing through it's origin and it's tip.

Most vectors are going to get knocked off their span during the transformation.

it'd be very coincidental if the place where transformed vector landed happens to be somewhere on that same span line.

But some especial vectors do remain on the same line / span.

The effect that some matrix has on some vector is that it just stretch it or squish it, like a scalar. (check comments below for scalar)

In this example:

The basis vector i^ is one such special vector. The span of i^ is x-axis

from the 1st column of matrix

| 3 1 |

| 0 2 |

we can see that i^ moves over to 3 times itself, still on that x-axis

what's more interesting is that, because of the way linear transformation works.

Any other vector on the x-axis is also just stretched by the factor of 3. and also remains on it's own span.

Another slightly sneakier vector that remains on it's own span during this transformation is [-1 ,1 ]

| -1 |

| 1 |

it ends up getting stretched by the factor of 2.

Linearity is going to imply that any other vector on this diagonal line spanned by the transformation is just going to get stretched out by a factor of 2.

for this transformation, following are all the vectors with the special property of staying on their span.

1. Those on the x-axis is stretched by factor of 3.
2. Those on diagonal line is stretched by factor of 2.
3. Any other vector is going to get rotated somewhat during the transformation

after transformation, the vector pink is knocked off it's original span.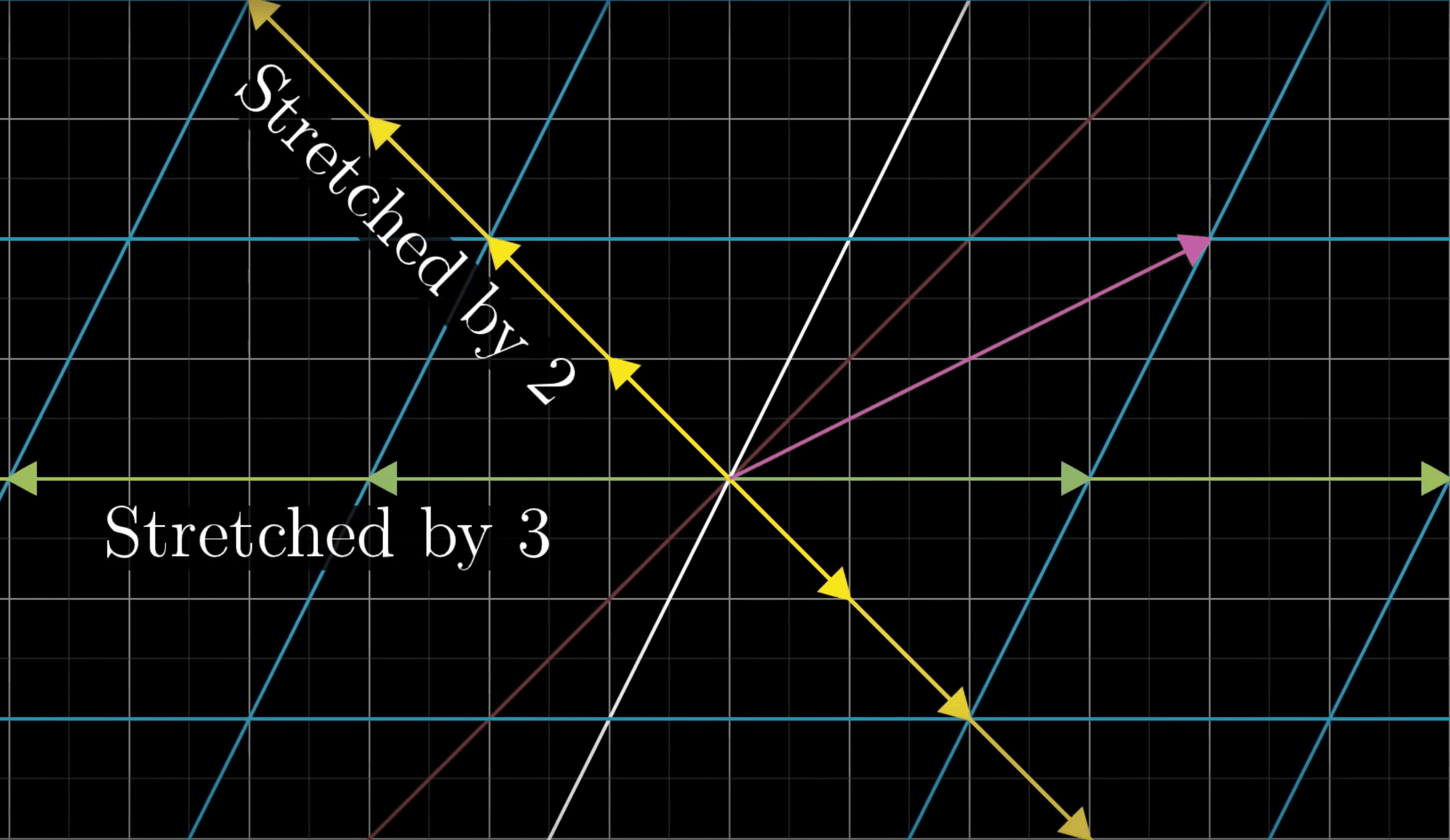

These especial vectors are called Eigenvectors of the transformation, and each Eigenvectors has associated with it what's called eigen value.

Eigen value = factor by which it's stretch or squished during the transformation

Mathematically, we express this as:

Av = λv

where

1. A is transformation matrix
2. v is the eigenvector
3. λ (lambda) is eigenvalue

We can also say that matrix vector product (A * V ) gives the same result as scaling the eigenvector v by some value of λ (lambda)

Av = λv

1. left hand side = matrix-vector multiplication
2. right hand side is scalar-vector multiplication.

Key points:

1. Eigenvectors are specific directions in which linear transformation acts by only stretching or compressing, not rotating.
2. Eigenvalues represents the factor by which the eigenvector is strechted or compressed.
3. A matrix can have multiple eigenvector-eigenvalue pairs.

Eigen Decomposition:

A fundamental concept in linear algebra that decomposes a square matrix into a set of eigen vectrors & eigen values.

This note is inspired from